Midterm 2 Review
PH142
Spring 2019
Navigating these slides
Welcome to the Midterm 2 Rpres. You can navigate these slides by
(1) Arrows by clicking the right and left arrows on your keyboard,
(2) Progress bar by clicking on the progress bar located at the very bottom of your browser (it's a slim blue bar),
(3) Manual entry by waiting a second, then typing in the slide number you wish to view within your URL address bar (change the last number in the URL to the slide number you wish to view.
If you cannot see the bottom of a slide try command-minus or control-minus.
Exam logistics
Bring your (1) ID, (2) calculator, and (3) intelligent self to your designated testing room at 8:00am sharp on the 22nd of March.
Note to Students
Please also consult lecture notes and your text. Many of you have been asking for sample problems. For understanding the material, textbook review exercises are great.
Use bCourses for all your statistical questions!
Good luck studying to all!
Material
PPDAC Application: You will still be tested on your ability to intepret studies!
Chapter 9, 10: Know when to apply your probability rules!
Chapter 11: Continuous Distribution, Normal
Chapter 12: Discrete Distributions, Binomial and Poisson
Chapter 13: Sampling Distribution, the distribution of your sample statistics
Chapter 14, 15: Hypothesis testing (CI's and z-test)
PPDAC Applications
The following PPDAC application slides are difficult to read on this Rpres. To study this topic, click on the following link to Google slides.
Bias
Bias
When the expected value based on a sample differs from the true underlying parameter value.
Take Home Questions:
- What does it mean for a statistic to be unbiased?
- Can a parameter be unbiased?
- What does unbiased-ness have to do with the sampling distribution? (See Chapter 13 slides.)
Probability
Chapter 9 and 10 are dense with formulas. Since you will most likely be putting these on your cheat sheet, your task is to be able to read word problems and apply the appropriate rules based on what the question is asking.
Look for patterns in language. Some words to look for are “given”, “and”, “or”, “both”, “neither”. Can you name more? Read some of your homework problems and see which words relate to which probability.
Chapter 9
Random samples eliminate bias from the act of choosing a sample, but they can still be wrong
This is because of the variability that results when we choose at random.
If the variation when we take repeat samples from the same population is too great (really big), we can't trust the results of any one sample.
Probablity
- The probability of any outcome of a random phenomenon is the proportion of times the outcome would occur in a very long series of repetitions.
- We call a phenomenon random if individual outcomes are uncertain but there is nonetheless a regular distribution of outcomes in a large number of repetitions.
Sample Space
- A sample space \( S \) of a random phenomenon is a set of all possible outcomes.
- An event on sample space \( S \) is an outcome (or a set of outcomes) of a random phenomenon. That is, an event is a subset of the sample space.
Probability Model
A probability model is a math description of a random phenomenon consisting of two parts: a sample space \( S \) and a way of assigning probabilities to events.
Remember doing this in your homework?
Probability Rules
Rule 1. The probability P(A) of any event satisfies \( 0\leq P(A)\leq 1 \).
Rule 2. If S is the sample space in a probability model, then P (S) = 1.
Rule 3. Two events A and B are disjoint (mutually exclusive) if they have no outcomes in common and so can never occur together.
If A and B are disjoint, \( P(A U B) = P(A) + P(B) \). This is the addition rule for disjoint events.
Rule 4. The Complement Rule. For any event A,
\( P(A^C) = 1 - P (A) \)
where \( P(A^C) \) is the probability that A does not occur.
Probability Rules
Take Home Question: Where does Rule 4 appear when we're using distributions?
Rule 4. The Complement Rule. For any event A,
\( P(A^C) = 1 - P (A) \)
where \( P(A^C) \) is the probability that A does not occur.
Notation
- The mean of a density curve is \( \mu \)
- The standard deviation of a density curve as \( \sigma \)
- The sample mean is denoted as \( \bar{x} \)
Discrete models
A probability model with a sample space made up of a list of individual outcomes is called discrete.
Example
e.g., Birth type: S = {vaginal, cesarean}
e.g., Daily soda consumption: S = {0, 1, 2, 3, 4+}
Relate this back to what you know about discrete data.
Continuous models
The sample space is now an entire interval of numbers:
S = {all numbers between 0 and 1}
Example
e.g., Annual income: S = {0 to \( \infty \)}
Relate this back to what you know about continuous data.
Density Curve
- A density curve describes/model the overall pattern of a distribution. (No real data perfectly match a density curve!)
- It has area exactly 1 underneath it.
- Only intervals of values have positive (non-zero) probabilities.
Question: Does the normal distribution have a density curve? Does the binomial?
Sampling with Code
The sample_n function can be used in this way. The iris dataset is built into R!
library(dplyr)
sample_2 <- sample_n(iris, size = 2)
sample_2
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 6.7 3.3 5.7 2.5 virginica
2 6.9 3.1 5.4 2.1 virginica
Sampling with Code
The sample_n function can be used in this way. The iris dataset is built into R!
sample_6 <- sample_n(iris, size = 6)
sample_6
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 6.5 3.0 5.2 2.0 virginica
2 5.8 2.7 4.1 1.0 versicolor
3 5.8 2.7 5.1 1.9 virginica
4 5.1 3.5 1.4 0.3 setosa
5 5.7 2.8 4.5 1.3 versicolor
6 5.6 2.5 3.9 1.1 versicolor
Chapter 10
Now, we're sliding into Chapter 10 material.
Dependence and Independence
Two events are independent if knowing that one event occurred does not change the probability that the other occurred
Multiplication Rule for Independent Events
Two events A and B are independent if knowing that one occurs does not change the probability that the other occurs. If A and B are independent,
\( P(A \cap B) = P(A)\times P(B) \)
Conversely, if this condition is not satisfied, then events A and B are dependent.
Conditional Probability
When P(A) > 0, the conditional probability of B, given A, is
\( P(B|A)=\frac{P(A\&B)}{P(A)} \)
General addition rule for any two events
For any two events A and B, \( P(A \cup B) = P(A) + P(B) - P(A \cap B) \).
The probability that both of two events A and B happen together can be found by:
This formula simplifies to \( P(A \cup B) = P(A) + P(B) \) when A and B are disjoint.
Example
Hearing impairment in dalmatians Congenital sensorineural deafness is the most common form of deafness in dogs and is often associated with congenital pigmentation deficiencies.
A study of hearing impairment in dogs examined over five thousand dalmatians for both hearing impairment and iris color. Being Impaired was defined as deafness in either one or both ears. Dogs with one or both irises blue (a trait due to low iris pigmentation) were labeled blue.
The study found that 28% of the dalmatians were hearing impaired, 11% were blue eyed, and 5% were hearing impaired and blue eyed.
Example
Hearing impairment in dalmatians Congenital sensorineural deafness is the most common form of deafness in dogs and is often associated with congenital pigmentation deficiencies.
A study of hearing impairment in dogs examined over 5000 dalmatians for both hearing impairment and iris color. Being Impaired was defined as deafness in either one or both ears. Dogs with one or both irises blue (a trait due to low iris pigmentation) were labeled blue.
The study found that 28% of the dalmatians were hearing impaired, 11% were blue eyed, and 5% were hearing impaired and blue eyed.
Example
Question Write up information from the prompt in probability notation.
Solution
\( P(I) = 0.28 \)
\( P(B) = 0.11 \)
\( P(B \cap I) = 0.05 \)
Example
Question What is the probability of dalmatians being either blue eyed or hearing impaired?
Solution
\( P(B \cup I) = P(B) + P(I) - P(B\cap I) = 0.11 + 0.28 - 0.05 = 0.34 \)
Example
Additional Questions for Home:
- What is the probability of a dalmatian being unimpaired and brown-eyed dog if it is neither hearing impaired nor blue eyed?
- Are \( B \) and \( I \) independent? Or dependent?
If this was difficult to answer, please refer to Sarah's Venn Diagram notes on bCourses.
General multiplication rule
\( P(A \cap B) = P(A)P(B|A) \). This is simply a rearrangement of the conditional probability formula.
This simplifies to \( P(A \cap B) = P(A) \times P(B) \) when A and B are independent events.
Bayes' Theorem
\( P(A|B)=P(A) \) if independent. But if they aren't…
\[ P(A|B) =\frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|A^c)P(A^c)} \]
\[ P(A|B) =\frac{P(A|B)P(B)}{P(B|A)P(A) + P(B|A^c)P(A^c)} \]
\[ P(A|B) =\frac{P(A \cap B)}{P(B|A)P(A) + P(B|A^c)P(A^c)} \]
Absolute frequencies and tree diagrams

Absolute frequencies and tree diagrams
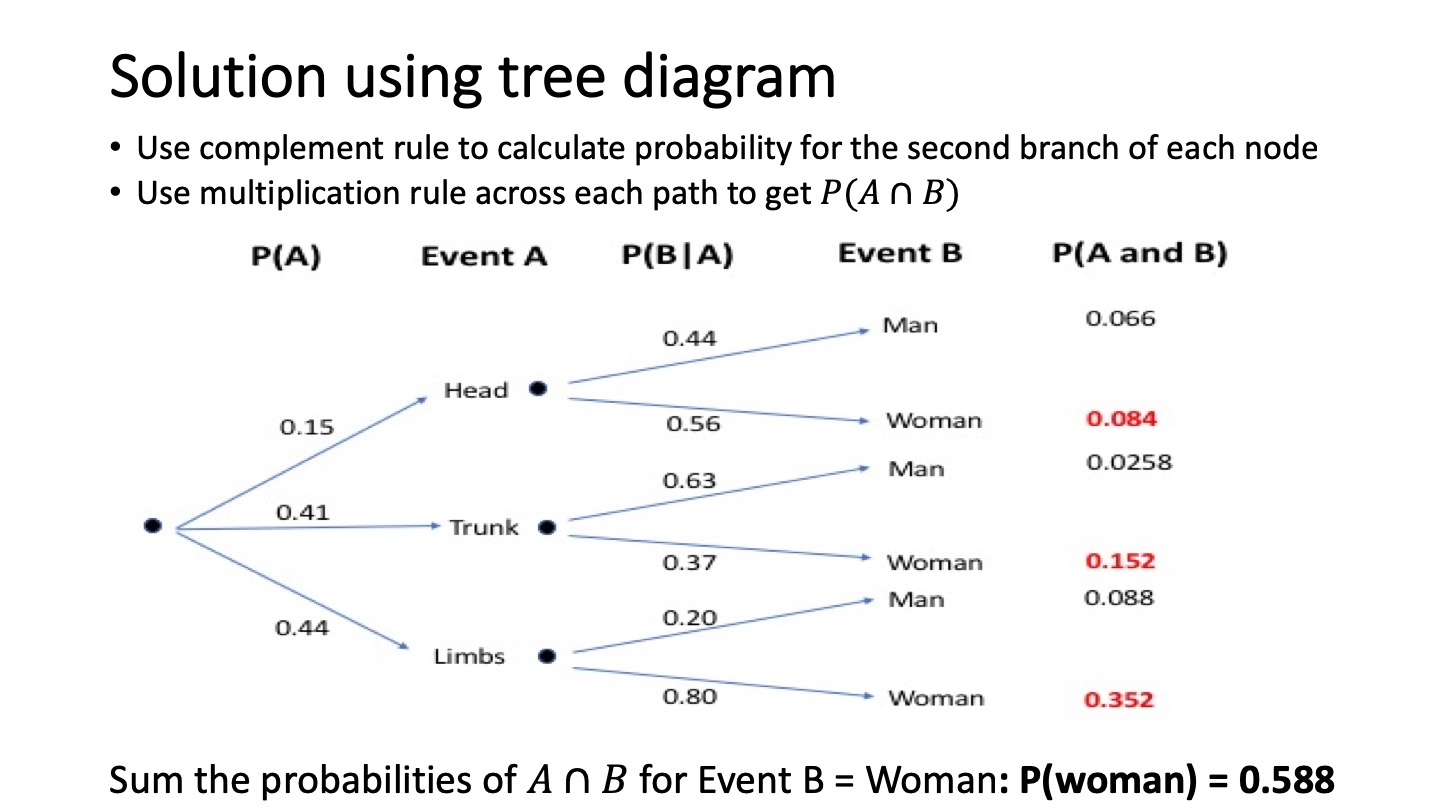
Absolute frequencies and tree diagrams

Distributions
A common question has been WHEN DO WE USE THESE DISTRIBUTIONS!? Well, sometimes our data tell a story that we see over and over again.
We can think of distributions as things that model patterns in data. If we see data that looks approximately normal or follows a recipe for the Binomial or Poisson(*), then we should definitely consider using the appropriate distribution. When we use a distribution like one of the named three above, we can end up saying a lot about our data. We can say the mean, the variance/standard deviation, and calculate probabilities.
(*) See the following Chapter 11 and 12 notes for these recipes.
Chapter 11: Normal Distribution
Recipe for Normal
- Goals: We want to find a probability for greater or less than or greater/equal, less/equal, but NEVER exactly equal to a single number
- The data are said to be normal or are assumed to be normal in the prompt
Question
What is the difference between normal and standard normal?
Example
According to basketball-reference.net, the mean height for NBA players is 6'7" = 79 inches. Suppose it is known that player height is normally distributed with a standard deviation of 4 inches. What is the probability of a ball player to be shorter than 6 feet?
Example
The prompt information translates to:
mu <- 79
sd <- 4
k <- 6*12
We can calculate this probability one way (without tables!).
pnorm(q=k, mean=mu, sd=sd)
[1] 0.04005916
All the [ ]norm functions are fair game!
Chapter 12: Binomial and Poisson Distributions
Refer to your homework assignments for practice problems!
Binomial
This is the formula for the Binomial distribution.
\[ P(X=k) = \Sigma_{k=0}^{n} \binom{n}{k}(p)^{k}(1-p)^{n-k} \]
Since you'll probably have this formula on your cheat sheet, what's more important is understanding what each of the pieces of the binomial distribution function.
As we said earlier, distributions are used to calculate means, variances, and probabilities of situations we see often! Think back to the Korean drama or pop song. They have well-known structures. So does the Binomial setting. Check if your data fit the Binomial setting.
Binomial
Recipe for Binomial
1. Goals: We want to find a probability, these are all fine: less than/equal/greater than/combo
2. You have some fixed amount of trials
3. Trials are independent
4. The probability of success is the same for each trial
5. There may be more assumptions, look for these at home.
Normal Approximation for the Binomial Distribution
- If we have a binomial distribution that satisfies the below properties, we can approximate the distribution as a normal distribution instead
- This allows us to use all the awesome properties we know about normal distributions (very convenient!)
Example
A shopper goes online Thursday mornings to attempt to purchase Supreme apparel and accessories. Due to the brand's popularity and limited supply, the shopper successfully purchases any item 1 in 10 times. What is the probability that the shopper will make 4 successful purchases after 10 independent purchase attempts? How about greater than 4?
Example
The prompt information translates to:
n_trials <- 10
k_success <- 4
probability <- 1/10
And we can calculate the first quantity “by hand” using the formula:
choose(n_trials, k_success)*(probability)^k_success*(1-probability)^(n_trials-k_success)
[1] 0.01116026
Example
The prompt information translates to:
n_trials <- 10
k_success <- 4
probability <- 1/10
Or we can use a special function:
dbinom(x=k_success, size=n_trials, prob=probability)
[1] 0.01116026
Example
The second quantity (the probability of greater than 4) can be found by using the Complement Rule.
1 - choose(n_trials, 4)*(probability)^(4)*(1-probability)^(n_trials-4) - choose(n_trials, 3)*(probability)^(3)*(1-probability)^(n_trials-3) - choose(n_trials, 2)*(probability)^(2)*(1-probability)^(n_trials-2) - choose(n_trials, 1)*(probability)^(1)*(1-probability)^(n_trials-1) - choose(n_trials, 0)*(probability)^(0)*(1-probability)^(n_trials-0)
[1] 0.001634937
Example
Or using another cool function that calculate the sum of probabilities from 0 to k.
1-pbinom(q=k_success, size=n_trials, prob=probability)
[1] 0.001634937
Or even more conveniently:
pbinom(q=k_success, size=n_trials, prob=probability, lower.tail=FALSE)
[1] 0.001634937
All the [ ]binom functions are fair game!
Poisson
This is the formula for the Poisson distribution.
\[ P(X=k) = e^{-\lambda}\frac{\lambda^k}{k!} \]
Recipe for Poisson
1. Goals: We want to find a probability, these are all fine: greater/less/equal/combo
2. Events occur independently.
3. The rate at which events occur is constant. The rate cannot be higher in some intervals and lower in other intervals.
3. There are more assumptions, look for these at home.
Example
San Francisco is known for its fog. In fact, the fog's name is Karl! We expect a warm, sunny, Karl-free day in San Francisco about twice per month.
Do this at home: What is the probability that we see more than 5 days of sun in San Francisco in a month? How about exactly 10?
Sampling Distributions
A sampling distribution is the distribution of estimates that we have for our parameter. In our case, we either make distributions of estimates for \( \mu \) or population proportion \( p \).
Chapter 13
Here's a motivating figure from the text. After you're done looking over this section, reflect on this figure and see if you can understand it all.
Law of Large Numbers
As \( n \) gets huge, our sampling distribution's mean will get closer and closer to the true population parameter value.
Law of Large Numbers
Example
Let's take a look at some NBA data that was scraped off of basketball-reference.com. We'll read in the csv.
western_conference <- read.csv("western_nba.csv")[,-1]
head(western_conference, 3)
Player millions team
1 Stephen Curry 37.45715 Golden State Warriors
2 Russell Westbrook 35.65415 Oklahoma City Thunder
3 Chris Paul 35.65415 Houston Rockets
mean(western_conference$millions)
[1] 6.500936
Law of Large Numbers
In the following blocks, we're going to take 100 samples of size \( n=2, 5, 30 \). Ignore the code that you have you never learned. Focus on the output.
Law of Large Numbers
Sampling with n=2
sample_means_2 <- do.call(rbind, lapply(1:100, function(x) sample_n_salaries(2)))
sample_means_2 %>% summarize(sampling_mean=mean(mean_salary))
sampling_mean
1 6.374358
Law of Large Numbers
Sampling with n=5
sample_means_5 <- do.call(rbind, lapply(1:100, function(x) sample_n_salaries(5)))
sample_means_5 %>% summarize(sampling_mean=mean(mean_salary))
sampling_mean
1 6.019269
Law of Large Numbers
Sampling with n=30
sample_means_30 <- do.call(rbind, lapply(1:100, function(x) sample_n_salaries(30)))
sample_means_30 %>% summarize(sampling_mean=mean(mean_salary))
sampling_mean
1 6.560197
Central Limit Theorem
As \( n \) gets huge, our sampling distribution itself will look more and more like a normal distribution.
Central Limit Theorem
Example
Recall the data from earlier.
head(western_conference, 10)
Player millions team
1 Stephen Curry 37.45715 Golden State Warriors
2 Russell Westbrook 35.65415 Oklahoma City Thunder
3 Chris Paul 35.65415 Houston Rockets
4 LeBron James 35.65415 Los Angeles Lakers
5 Paul George 30.56070 Oklahoma City Thunder
6 Mike Conley 30.52112 Memphis Grizzlies
7 James Harden 30.43185 Houston Rockets
8 Kevin Durant 30.00000 Golden State Warriors
9 Paul Millsap 29.73077 Denver Nuggets
10 Damian Lillard 27.97769 Portland Trail Blazers
Central Limit Theorem
Exploring the Population (“The Underlying Distribution”)
This is the distribution of the population salaries.
Central Limit Theorem
Exploring the Population (“The Underlying Distribution”)
What is the mean parameter \( \mu \) of the population? We can calculate this by hand or by a function. Focus on the by hand calculation.
Here's the “by hand” calculation. The following functions may seem new to you, but think intuitively instead of code-wise. We have a data on all of the salaries, then we add all the salaries up, then divide by the number of salaries we have to get the average.
vector_of_salaries <- western_conference$millions
sum(vector_of_salaries) / length(vector_of_salaries)
[1] 6.500936
Central Limit Theorem
Exploring the Population (“The Underlying Distribution”)
What is the mean parameter \( \mu \) of the population? We can calculate this by hand or by a function. Focus on the by hand calculation.
Here's the dplyr solution.
library(dplyr)
western_conference %>% summarize(mu=mean(vector_of_salaries))
mu
1 6.500936
Let's see what our sample distribution looks like for several choices of \( n \).
Central Limit Theorem
Sampling with n=2
ggplot(sample_means_2, aes(x=mean_salary)) +
geom_histogram(binwidth=0.7) +
scale_x_continuous(limits = c(0, 40))
Central Limit Theorem
Sampling with n=5
ggplot(sample_means_5, aes(x=mean_salary)) +
geom_histogram(binwidth=0.5) +
scale_x_continuous(limits = c(0, 40))
Central Limit Theorem
Sampling with n=30
Visually, the sample size of \( n=30 \) is the most symmetric.
ggplot(sample_means_30, aes(x=mean_salary)) +
geom_histogram(binwidth=0.5) +
scale_x_continuous(limits = c(0, 40))
As \( n \) gets larger, then we see the sampling distribution get less skewed and more like the normal curve.
Sampling Distribution Means and Variances
Sampling distributions have means and variances that can be calculated as specified below!
mean variance
counts x-bar sd/sqrt(n)
proportions p (p(1-p))/n
Question: What is the relationship between variance and standard deviation?
Question for Home: What assumptions go along with sampling distributions and their normalities? Check the chapter.
Chapter 14, 15
In these chapters, we introduce inference. Inference is the process of drawing conclusions about a population based on a sample. We will do this by testing hypotheses using confidence intervals and z-tests. Notice that the two methods to test hypotheses will bring about the same conclusions.
Hypotheses
In inference, we're normally interested in hypotheses like:
\[ H_0: \mu = 5 \\ H_1: \mu \neq 5 \]
The first hypothesis is called your null hypothesis which specifies the status quo belief. The other hypothesis is called the alternative hypothesis.
A confidence interval can be used to test hypotheses. We also have covered using a z-test.
Confidence Intervals
- A confidence interval can provide evidence for or against the null hypothesis.
- A confidence interval is of the form estimate \( \pm \) (margin of error).
- Margin of error is your critical value \( z_{\alpha/2} \) times (standard error).
\[ \bar{X} \pm z_{\alpha/2}\text{(SE)} \]
- For a 95% CI, \( z_{\alpha/2}=1.96 \). For a 90% CI, \( z_{\alpha/2}=1.64 \). In general, increasing your confidence level will make your intervals wider (and your critical value bigger).
- CI's are normally reported in this fashion \( (\text{LB}, \text{UB}) \)
Confidence Intervals
The interpretation of a CI is very specific! Do not say that you are 95% sure that our true parameter is within our interval. Instead, this:
Interpretation Using a method that creates confidence intervals that capture the true parameter 95% of the time, we constructed the interval \( (\text{LB}, \text{UB}) \). This means that 95% of such intervals will contain our true parameter.
Confidence Intervals
Concluding based on a CI How do we test hypotheses based on a CI? Recall our arbitrary hypotheses.
\[ H_0: \mu = 5 \\ H_1: \mu \neq 5 \]
- If the null hypothesized parameter is not in our interval, then we can say that we reject \( H_0 \). That is, if 5 is not in the interval that we created, then we reject.
- When we reject \( H_0 \), we do not accept \( H_1 \).
Z-testing
The general procedure for running a z-test (after identifying the parameter of interest and ensuring conditions are met) is:
1) State the null and alternative hypotheses
2) Calculate the z test statistic
3) Use the test statistic to find the p-value
4) Generate a conclusion about your hypotheses using your p-value (reject vs. fail to reject the null)
Remember that we run a z-test when we know the true population standard deviation, \( \sigma \). You would be provided this value on the midterm.
Z-test conditions
The conditions to run a z-test include:
1) The sample is a SRS (simple random sample)
2) The data comes from a Normal distribution/population
3) The true, population standard deviation \( \sigma \) is known
Step 1: Hypotheses
Your hypotheses can be one-sided or two-sided.
- An example of a two-sided test is:
\[ H_0: \mu = 3, H_a: \mu \neq 3 \]
- Some examples of a one-sided test are:
\[ H_0: \mu = 3, H_a: \mu > 3 \]
or
\[ H_0: \mu = 3, H_a: \mu < 3 \]
Sometimes you are explicitly told what kind of a test to run. Other times, it is your responsibility to figure out which direction you test based on context from the word problem.
Step 2: Z-value calculation
The formula for the z test statistic is:
\[ z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}} \]
where:
- \( \bar{x} \) is the sample mean (aka the statistic)
- \( \mu \) is the population mean that is part of the hypothesis (aka the parameter)
- \( \sigma \) is the population standard deviation
- n is the sample size
Step 3: Finding the p-value
Once we have our z-value, we can find the p-value. To help find the p-value, sketch the standard Normal curve and mark on it the observed value of z. Depending on whether you are performing a one-sided test or a two-sided, this will determine in which direction you calculate the p-value/probability:
Here is a visual to illustrate the differences
#
Use pnorm() functions to calculate your p-value. Remember we are working with a Standard normal.
Step 4: Interpreting p-values
Once we have our p-values, we can relate these back to our hypotheses and come to a conclusion. Be careful interpreting p-values! The p-value represents the probability, assuming that \( H_0 \) is true, that the test statistic would take a value at least as extreme (in the direction of \( H_a \)) as that actually observed. Note that the p-value is NOT the probability that the null hypothesis is true.
The smaller the p-value, the stronger the evidence against \( H_0 \) provided by the data.
As a general rule of thumb, we:
- reject \( H_0 \) when p-value < \( \alpha \)
- fail to reject \( H_0 \) when p-value > \( \alpha \)
where \( \alpha \) is typically set to 0.05 (unless otherwise stated in the problem).
Step 4: Interpreting p-values
Correct interpretations:
If p < \( \alpha \): We found a p-value of p = [p-value]. This is less than our cut-off value of \( \alpha \) = [\( \alpha \)]. So we reject the null hypothesis that [null hypothesis] and have evidence to support the alternative hypothesis that [alternative hypothesis]
If p \( \geq \alpha \): We found a p-value of p = [p-value]. This is greater than our cut-off value of \( \alpha \) = [\( \alpha \)]. so we fail to reject the null hypothesis that [null hypothesis] and do not have evidence to support the alternative hypothesis that [alternative hypothesis].
Example (try on your own)
An environmentalist group collects a liter of water from each of 45 random locations along a stream. The mean amount of dissolved oxygen per liter is 4.62 mg. Suppose that we know that dissolved oxygen varies among locations according to a Normal distribution with \( \sigma \) = 0.92 mg. Is this strong evidence that the stream has a mean oxygen content of less than 5 mg per liter? Perform a hypothesis test by completing the following steps:
1) State your null and alternate hypotheses (hint: is it one-sided or two-sided?):
\[ H_0: \]
\[ H_a: \]
Example (try on your own)
2) Calculate the z-statistic:
\[ z = \]
3) Find the p-value. Express this using probability notation, and write the proper pnorm() function to use.
Probability notation:
\[ p-value = \]
Code:
pnorm( )
4) Interpret your p-value.
Type I and II Errors
Types I Error
Critical value
Types II Error
Power
Power
Take Home Questions
- What is a parameter? What is a statistic?
- If P(B)=3% and P(A)=4% and are independent of one another, what is \( P(A \cap B) \)? Hint: can you multiply two percentages?
- If you're asked for the P(+), does this include both true and false positives?
Extra
Supplementary material available here.