Lab 12. Regressing toward mediocrity.

History

Francis Galton was the first to describe the regression line, sometime in the late 1800's.
He was practicing eugenics. Francis Galton thought it would be better if people were taller. If you're interested, see Galton's paper. Where do you "stand" on this graph of mediocrity?

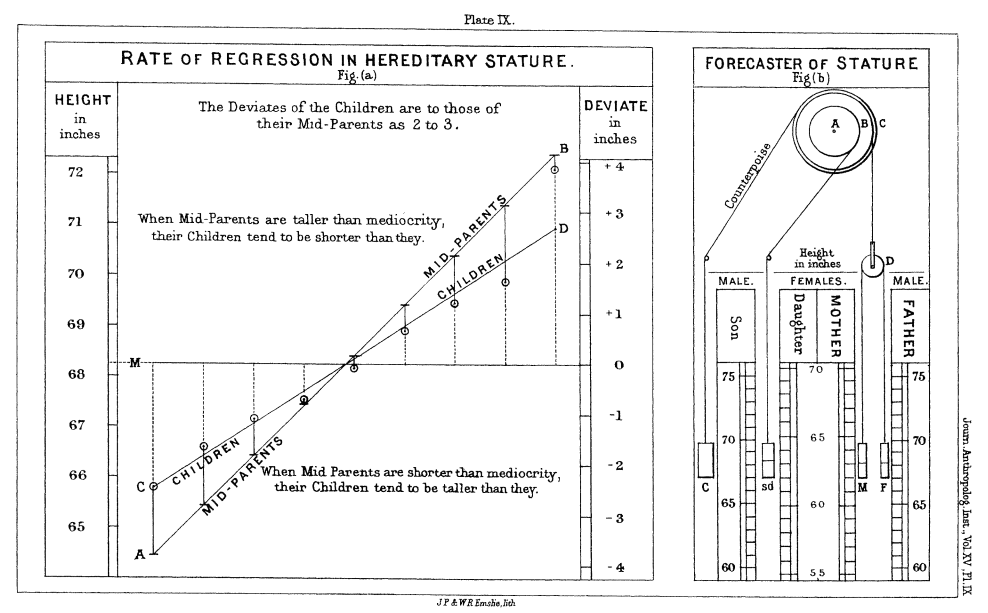</font>

Review

We have seen regression before in this class.
You have (1) seen scatterplots, (2) ran lm() and wrote a regression line based on the output, (3) interpreted the slope, intercept, $R^2$, (4) spotted outliers.

Vocabulary

Causal effect v. association An association does not imply causal. The regression model will tell you about association between two variables.

We call these variables explanatory and response variables, unfortunately. We have the Xplanatory and the response as Y.

Once we have a linear model based on our data, we can calculated predicted or fitted values. We can subtract our predicted values from our observed values to calculate our residuals. </font>

Regression Test

We are testing hypotheses about the slope and the intercept.

Assumptions

These assumptions are different than the ones in the book. To test these assumptions, we look at graphs.

  • $x, y$ linear in scatterplot
  • Residuals are normally distributed.
  • Independent observations
  • Standard deviation of the response variables are the same for all values of x
</font>

The test itself

These are assumptions for $\beta_1$.

$H_o: \, \beta_1 = 0$
$H_1: \, \beta_1 \neq 0$

Why would we do this? </font>

In [1]:
library(MASS)
head(Boston)
crimzninduschasnoxrmagedisradtaxptratioblacklstatmedv
0.0063218 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98 24.0
0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14 21.6
0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03 34.7
0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94 33.4
0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 36.2
0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21 28.7

Here's the fitted model plotted on top of the scatterplot.

In [7]:
library(ggplot2)
ggplot(augment_Boston, aes(nox, medv)) +
    geom_point() +
    ggtitle("Scatterplot of Median House Price v. Air Pollution") +
    ylab("Median House Price") +
    xlab("Air Pollution (Nitrogen Oxide)")

Let's fit a model. Use lm.

In [5]:
lm_Boston <- lm(medv ~ nox, data = Boston)
tidy(lm_Boston)
termestimatestd.errorstatisticp.value
(Intercept) 41.34587 1.811192 22.82800 9.866245e-80
nox -33.91606 3.196337 -10.61091 7.065042e-24

Interpret the slope.

In [3]:
library(broom)
library(ggplot2)
library(dplyr)
library(tidyr)

Attaching package: ‘dplyr’

The following object is masked from ‘package:MASS’:

    select

The following objects are masked from ‘package:stats’:

    filter, lag

The following objects are masked from ‘package:base’:

    intersect, setdiff, setequal, union
In [8]:
# GIVES ASSOCIATED "REGRESSION VALUES" WITH EACH COORDINATE
augment_Boston <- augment(lm_Boston)
In [9]:
head(augment_Boston)
medvnox.fitted.se.fit.resid.hat.sigma.cooksd.std.resid
24.0 0.538 23.09904 0.3738461 0.9009631 0.002017389 8.331520 1.186674e-05 0.1083546
21.6 0.469 25.43924 0.4603695 -3.8392447 0.003059265 8.329853 3.274492e-04-0.4619693
34.7 0.469 25.43924 0.4603695 9.2607553 0.003059265 8.321347 1.905220e-03 1.1143297
33.4 0.458 25.81232 0.4821178 7.5876787 0.003355137 8.324722 1.403528e-03 0.9131470
36.2 0.458 25.81232 0.4821178 10.3876787 0.003355137 8.318690 2.630512e-03 1.2501159
28.7 0.458 25.81232 0.4821178 2.8876787 0.003355137 8.330619 2.032830e-04 0.3475207

Here's the fitted model plotted on top of the scatterplot.

In [10]:
ggplot(augment_Boston, aes(nox, medv)) +
    geom_segment(aes(xend = nox, yend = .fitted), color="darkgrey") +
    geom_point(col="midnightblue") +
    ggtitle("Look at the residuals") +
    geom_smooth(method = "lm", se = F, col="midnightblue")
In [11]:
ggplot(augment_Boston, aes(nox, medv)) +
    geom_point(col="darkgrey") +
    ggtitle("Look at the line") +
    ylab("Median House Price") +
    xlab("Air Pollution (Nitrogen Oxide)") +
    geom_smooth(method = "lm", se = F, col="midnightblue")
In [12]:
ggplot(augment_Boston, aes(sample = .resid)) + 
  geom_qq() + 
  geom_qq_line(col="darkgrey")
In [13]:
ggplot(augment_Boston, aes(y = .resid, x = .fitted)) + 
  geom_point(col="midnightblue") +
  geom_hline(aes(yintercept = 0)) +
  labs(y = "Residuals", x = "Fitted values", title = "(c) Fitted vs. residuals")
In [14]:
reshape <- augment_Boston %>% dplyr::select(.resid, medv) %>%
  gather(key = "type", value = "value", medv, .resid)

ggplot(reshape, aes(y = value)) +
  geom_boxplot(aes(fill = type)) +
  ggtitle("Look at the variation in residuals and in the response") +
  scale_fill_manual(values = c("darkgrey", "gold"))

References

About R^2

Reading for You

Regression Test